Discrete Domain Analysis

The discrete approach simplifies the problem, making it easier to solve. Let’s assume that the rope stretches instantaneously at the end of each second. This slight modification gives the ant a fairer chance compared to the original scenario. To generalize the problem, let ‘t’ denote time.

At the outset, when t = 0 seconds, the rope's initial length is represented as ‘l’ units, and the ant starts at a position of x = 0 units (the left end of the rope). As the clock begins, the ant crawls at ‘a’ units per second while the rope stretches at ‘v’ units per second.

Now, let’s delve deeper into how we can mathematically analyze this situation.

The Mathematical Framework of the Paradox

The ant's goal is to reach the end of the rope, initially positioned at ‘l’ units. However, every second, this target moves in the x-direction at a rate of ‘v’ units per second.

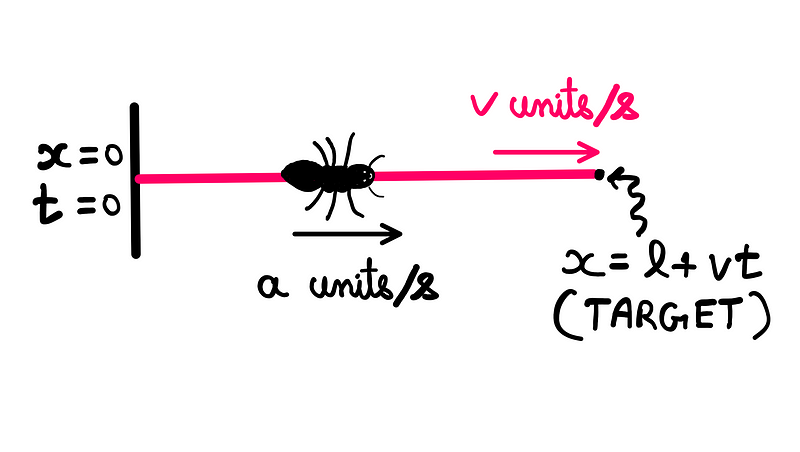
Thus, the target position at any time ‘t’ can be calculated as follows:

At the conclusion of the first second, the ant has covered ‘a’ units, while the target has moved to x = l + (v*1) = (l + v) units. Following this logic, at the end of two seconds, the ant would have traveled another ‘a’ units, and the target would be at x = l + (v*2) = (l + 2v) units.

Consequently, the ratio of the distance covered by the ant, denoted as F(t), can be described as follows:

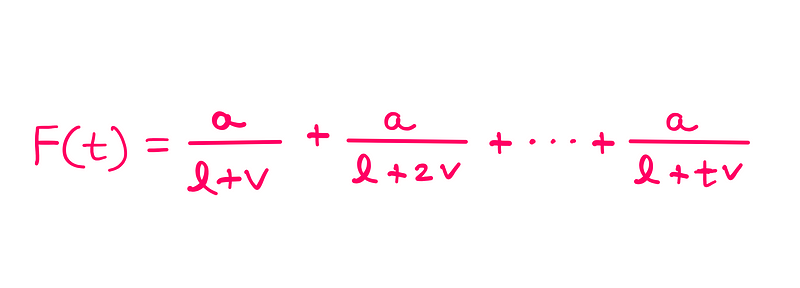
For the ant to succeed in reaching its destination, F(t) must be equal to or exceed ‘1’.

To investigate what occurs at t = k seconds, we represent this series with the equation:

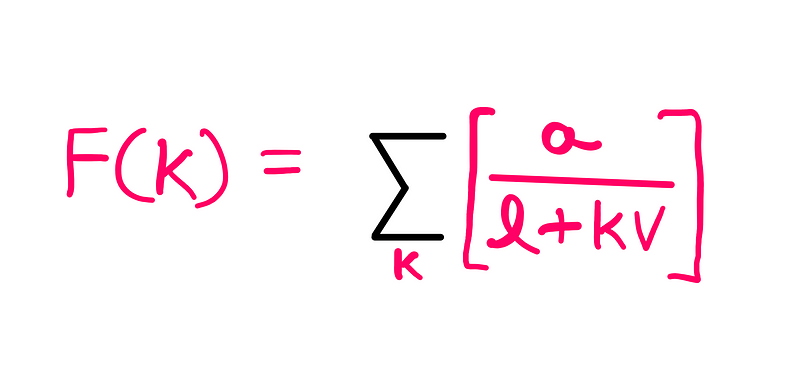
Let's enhance F(k) by including the ‘l’ term in the denominator multiplied by ‘k’, resulting in a new ratio G(k). As long as k is greater than zero, it follows that F(k) ≥ G(k) for k > 0.

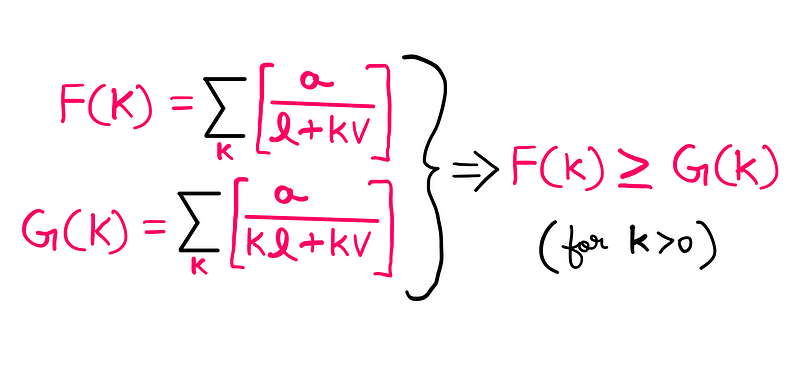
From this relationship, we can conclude that if G(k) reaches at least a value of ‘1’ for some ‘k’, then F(k) must also be at least that value. By factoring out ‘k’, we obtain:

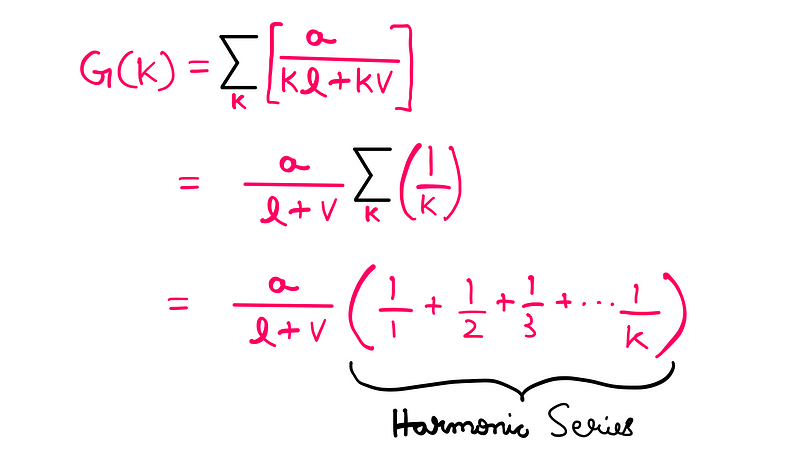
This series is known as the harmonic series, which diverges. For further understanding of convergence and divergence, refer to my essay on limits.

Given that we are dealing with a divergent series, there is no upper limit, suggesting that there exists a value of ‘k’ for which G(k) approaches 1:

Thus, the ant will eventually reach the end of the rope, provided it has sufficient time.

Continuous Domain Solution

While the continuous domain can also address this problem using calculus, it involves more complex mathematics, which I plan to cover in a future calculus series.

For now, it suffices to say that with a = 1 cm/s, v = 1 km/s, and l = 1 km, the solution yields:

k = (e¹????? — 1) ≈ 2.8 * 10³² seconds.

To put this into perspective, the estimated age of our universe is about 4 * 10¹⁰ seconds. Hence, we have a long wait ahead before the ant reaches the end of the rope (roughly 2.8 * 10³² km).

Intuition Behind the Paradox

When we manipulate the numbers and lower the scales, we can visually interpret the outcome. In the example below, the rope expands at a rate of 2 cm/s from an initial length of 4 cm. The red dot (representing the ant) crawls at 1 cm/s and reaches the end of the rope in 12.8 seconds.

This paradox serves as a compelling analogy for how light from distant galaxies travels through our expanding universe. The universe acts as the stretching rope, while the light beam symbolizes the ant.

It is noteworthy that light may never reach the far edge of our universe due to its accelerating expansion! The problem we analyzed assumed constant rates.