Section 1.1: The Big Dipper Explained

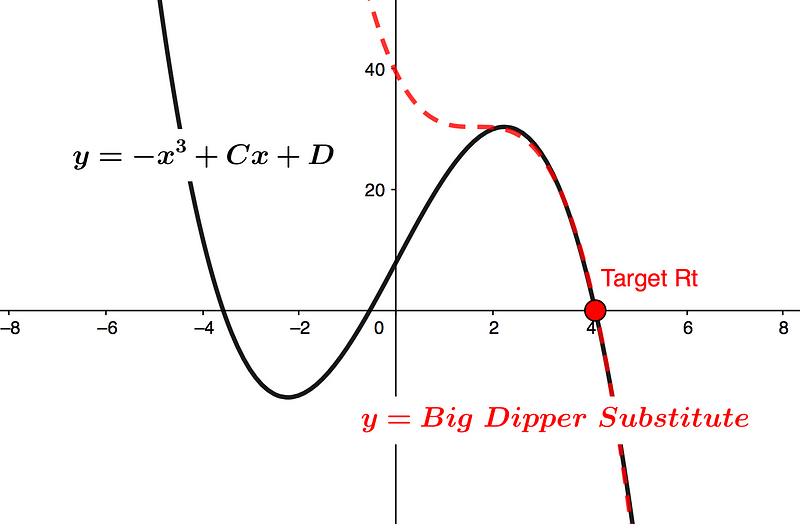
The genetic function y=-2x³+D, depicted in red in Graph 1 below, represents all depressed cubics y=x³+Cx+D. It is effective in tracing Turning Points (Tps) and not only aids in designing cubics with specific Tps but also provides a straightforward formula for determining the x coefficient C and calculating roots when Tp(y)=0 at the shared Root Intercept C.

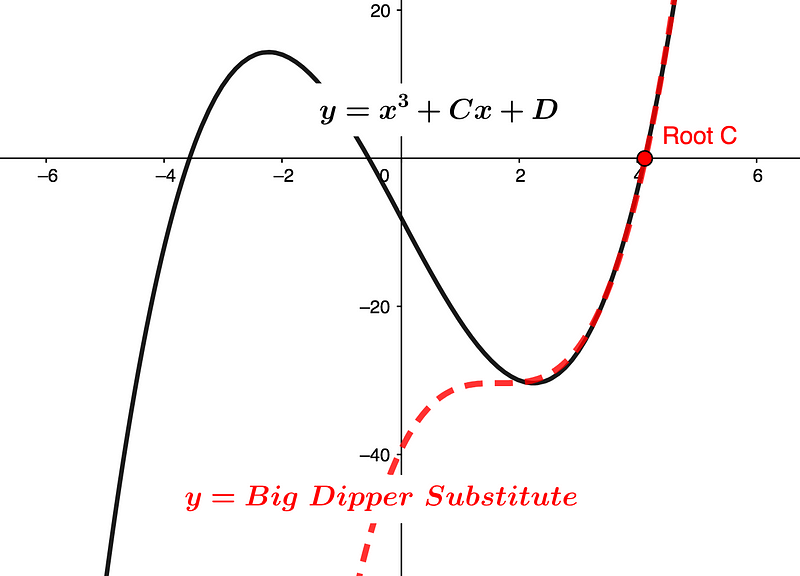
Note: Throughout this discussion, unless stated otherwise, the coefficient A for x³ is assumed to be +1, as this does not alter the roots when other values are divided across the function. When A=-1, Big Dipper’s coefficient changes to +1.

Section 1.2: Root Applications: Flipped and Dropped

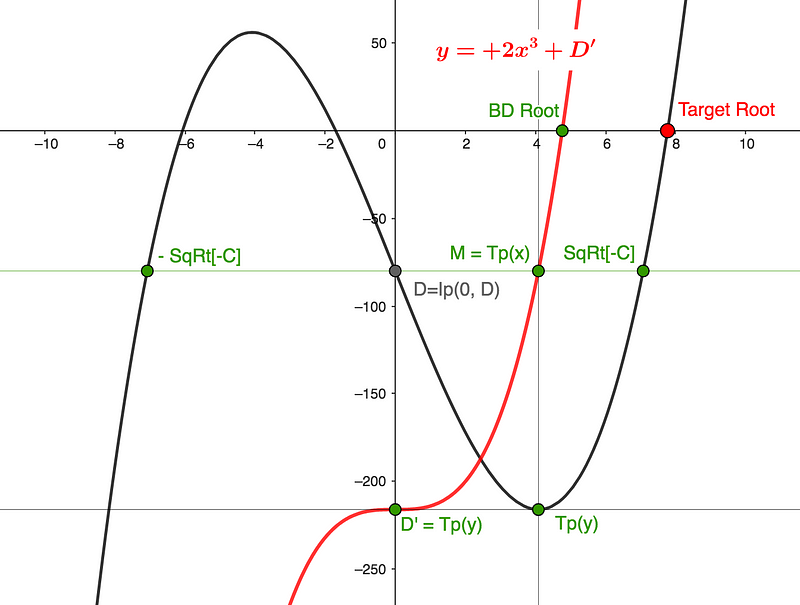
Considering any of the hybrids shown in Graph 1 (featuring the same x³ and D, but varying C values), we can intuitively understand that flipping their common Big Dipper to y=+2x³+D and adjusting the constant to D’=Tp(y) (at the Turning Point level of the function) allows us to approximate their profiles, as illustrated in Graph 2.

Key Metrics

The Inflection Point Ip(0, y)=D is established, and all intercepts shown in green can be calculated easily. The values of ±√[-C] represent the roots when D=Ip(y). The BD Root is determined from 0=2x³+D’, and significantly, M=Tp(x) as the Big Dipper traces all Tps from the subject cubic's Ip. (Visualize flipping and raising it back as shown in Graph 1; it will intercept Tp(y)).

Lateral Shift

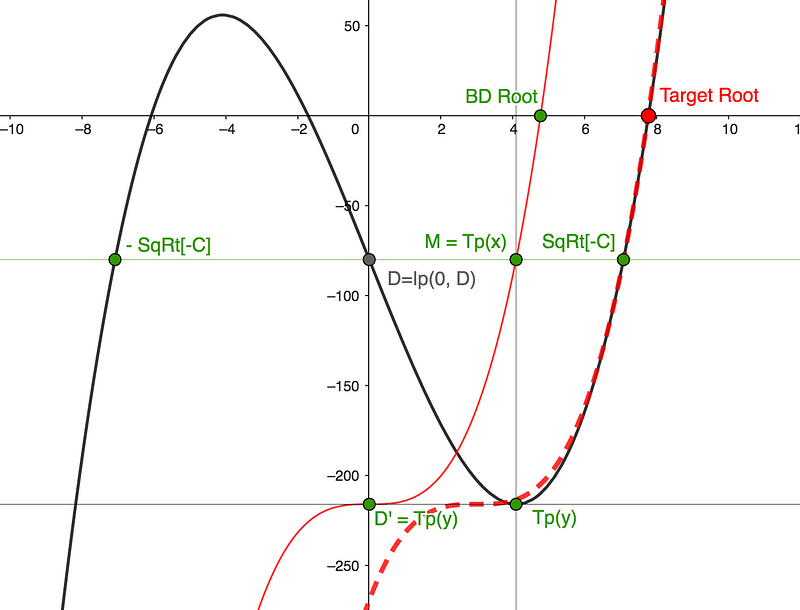
Next, envision shifting the dropped Big Dipper laterally, represented by the dashed red line, from the Intercept M=Tp(x) to √[-C]. The profile approximation becomes evident, as shown in Graph 3.

Subsection 1.2.1: Substitution Math

By moving the Big Dipper from Intercept M=Tp(x) to Intercept √[-C], we can transpose the easily calculated BD Root to approximate the Target Root. Therefore:

Target Root = BD Root + √[-C] - Tp(x)

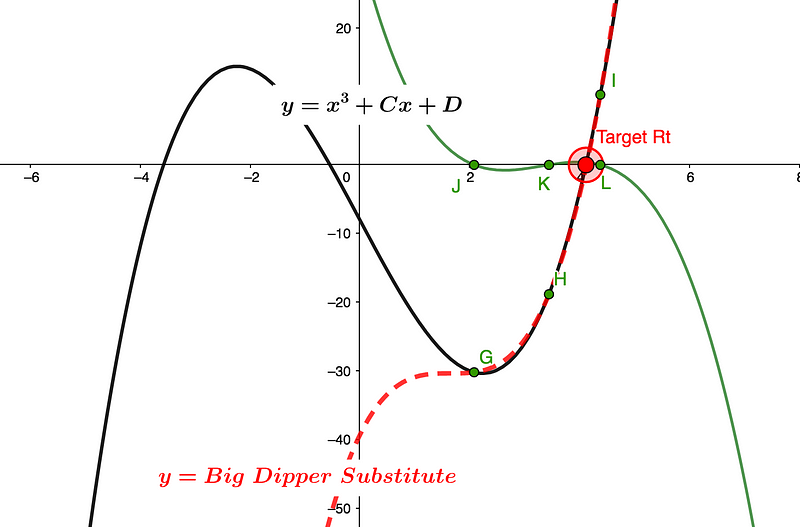
A significant benefit of this method over other root approximation techniques is its capacity to cover a wide range of roots despite changes in Cx and D. This close fit is applicable across most of the Tp(y) range, as highlighted by the intercepts G, H, and L of the two functions in green in Graph 4.

Extensions: Flipped Cubics

This root approximation method can also be applied to flipped cubics, as shown in Graph 5. The genetic Big Dipper y=+2x³+D maintains a positive coefficient of +2 and conforms to the subject cubic when transposed.

Design Parameters

Having clarified the positioning and application of Big Dipper for root analysis, its real potential may lie in robotics, where it can simplify algorithms that trace roots amid design changes in x coefficient C and constant D.

If you are interested in AI, you might find it beneficial to align the Big Dipper on the Y-Axis to match design constants and coefficient C related Tp(y)’s, as the roots will respond predictably, as depicted in Graph 6.

The General Case: Applying Big Dipper Substitution

Now that we've grasped the fundamentals of Big Dipper substitution, we are equipped to apply it to the general case where, unlike many approximation methods, we do not need to depress the cubic!

It is essential to understand that the Big Dipper, similar to all cubics, retains its shape regardless of repositioning in the X-Y grid. This substitution method is feasible because both cubics show considerable conformity, allowing us to apply it to the BD Root for the Target Root without concern for the actual relative spacing of their respective Ip(x)’s. An example will clarify this further.

Example: Standard Cubic

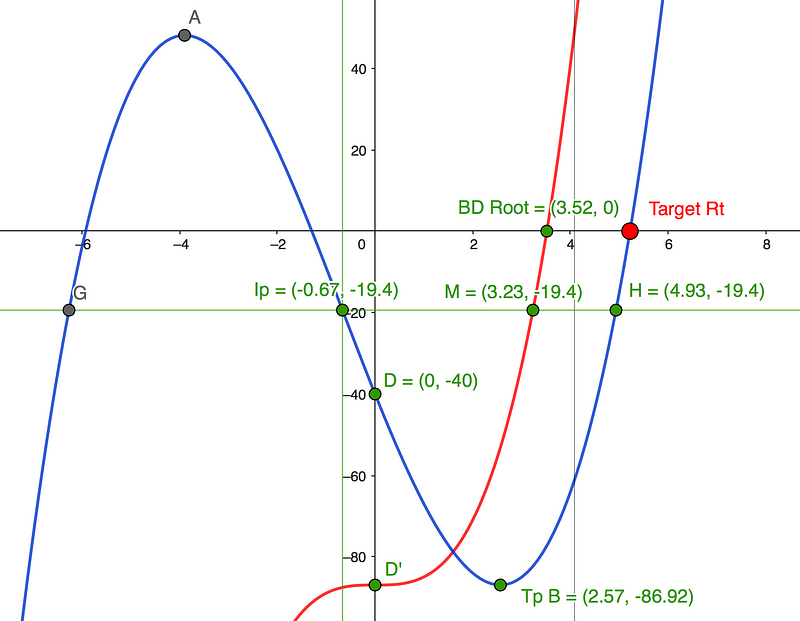
Consider the standard cubic y=x³+2x²-30x-40, as shown in blue in Graph 7 below.

The intercepts and BD Root, shown in green, are easily calculable. Note that the Big Dipper Constant D’=Tp(y) remains consistent. Intercept M=CubeRt[67.52/2]=3.23.

In this case, we do not need to perform the shift math as with standard cubics, although we must calculate Intercept H, which requires using the Extended Quadratic Equation (see below). Factor L=-Ip(-0.67) represents the hypothetical root if the Ip(y)=Ip(-19.4) were raised, introducing a new constant D=-40+19.4=-20.6.

Thus, we find:

Target Root = H - M + BD Root = 4.93 - 3.23 + 3.52 = 5.22, which aligns well with the actual root of 5.22.

Remaining Roots

The other external root can be easily derived using the same Big Dipper due to the rotational symmetry of cubics around the Inflection Point Ip(x, y). The internal root can be found by subtracting the sum of the factors from the x² coefficient B.

Alternatively, the remaining roots of the cubic function can be obtained through the Extended Quadratic Equation I discussed previously in "Cubic Polynomials — A Simpler Approach":

Where Factor L=-Root x, A, and B are the standard x^n coefficients, and D is the constant. This equation applies regardless of which of the three roots you input as Factor L.