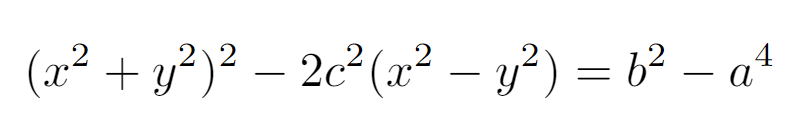# Exploring the Enigma of the Lemniscate of Bernoulli
Written on
Chapter 1: The Allure of the Lemniscate
Mathematics is a realm brimming with fascinating shapes, patterns, and equations that both captivate and inspire. One particularly intriguing figure is the lemniscate of Bernoulli, a geometric wonder named after the Swiss mathematician Jacob Bernoulli. In this article, we will delve into the enchanting world of the lemniscate, examining its definition, unique characteristics, and the mathematical principles that underlie this remarkable curve.
A Curve Steeped in History
The lemniscate of Bernoulli, an eye-catching figure-eight shaped curve, was first identified in 1694 by Jacob Bernoulli as a specific instance of the broader family of Cassini ovals. Its name is derived from the Latin term “lemniscatus,” meaning “adorned with ribbons,” which beautifully reflects the curve's intricate and elegant design. Throughout the centuries, this mesmerizing shape has drawn the attention of mathematicians, artists, and philosophers, marking its significance in both mathematics and aesthetics.
Defining the Lemniscate of Bernoulli
The lemniscate of Bernoulli can be expressed using polar coordinates. For a fixed point O, its equation is given by:
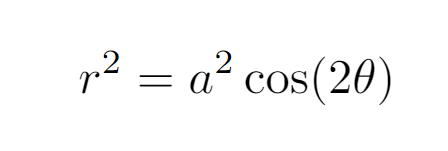
In this equation, r represents the distance from point O to any point on the curve, a is a constant that determines the size of the lemniscate, and θ is the angle formed between the positive x-axis and the line connecting point O to the point on the curve.
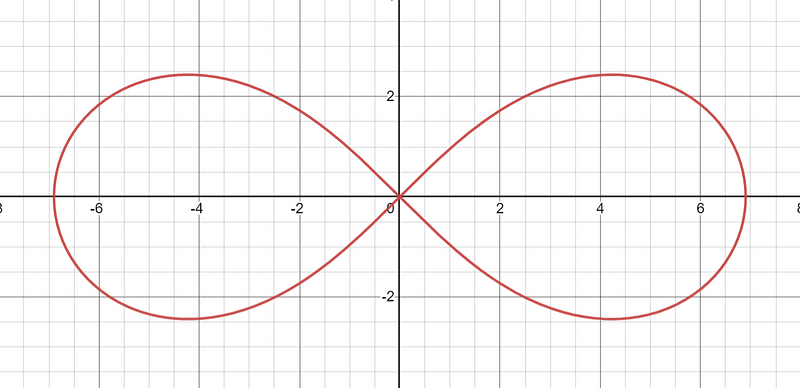
Examining the Properties
Now, let's explore some fascinating properties of the lemniscate of Bernoulli:
- Symmetry: The lemniscate exhibits reflectional symmetry across both the x-axis and y-axis, along with rotational symmetry of order 4. This means that the curve remains unchanged when rotated by 90 degrees.
- Bounded Area: The area enclosed by the lemniscate can be calculated through the following integral:
The integral is derived by computing the area of one side and then doubling the result to obtain the total area. A fun challenge for you could be to solve this integral!
- Arc Length: The length of one loop of the lemniscate can be determined using elliptic integrals, leading to the following formula:
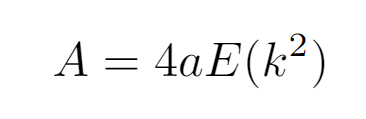
Here, E(k²) denotes the complete elliptic integral of the second kind, with k² = 1/2.
Applications and Related Curves
While the lemniscate of Bernoulli may not have direct applications in everyday scenarios, it has inspired various mathematical concepts. For instance, the lemniscate function is defined by the arc length of the lemniscate itself, and the lemniscate constant is derived from the complete elliptic integral of the second kind.
Moreover, the lemniscate is a particular case of the broader category of Cassini ovals, defined by the equation:
In this equation, ‘a,’ ‘b,’ and ‘c’ are constants. When a = b, the Cassini oval simplifies into a lemniscate.
As an interesting side note, the lemniscate can also be visualized as the envelope of circles that are centered on a rectangular hyperbola and pass through the hyperbola's center.
And that concludes our exploration of this remarkable curve. Isn’t it amazing? What are your thoughts? Feel free to share in the comments below; I’m eager to hear from you!
Explore the Lemniscate of Bernoulli with GXWeb in this engaging video.
Dive deeper into the Lemniscate of Bernoulli with GXWeb, perfect for math enthusiasts!
Math Puzzles
The finest math puzzles available on Medium, covering various topics such as algebra, geometry, calculus, and number theory. Share this with your friends!
Thank you for reading! If you found this article insightful, please show your appreciation with a clap.
If you feel generous, consider supporting my writing by buying me a coffee. Your support means a lot to me!
With gratitude, Bella