Chapter 1: Introduction to Complexity Theory

As data scientists and developers, we strive to devise innovative solutions to various challenges we encounter. This involves crafting algorithms, writing code, and conducting tests on different scenarios related to the problems at hand.

A crucial part of this workflow is identifying the type of problem and categorizing it. This classification helps determine whether the issue we’re facing is solvable before diving deeper into the development phase. Complexity theory is a branch of computer science focused on organizing problems into categories that indicate their solvability. Throughout your journey as a data scientist, programmer, or computer science enthusiast, you’ve likely encountered phrases like, "this is an NP problem," "this can be solved in P time," or "NP does not equal P!"

But what do these classifications truly signify? How can we discern which problems can be solved and which cannot? If a problem is deemed unsolvable, what alternatives do we have for approaching it?

Chapter 2: Understanding Complexity Classifications

This article aims to clarify these queries and enhance your comprehension of various complexity classifications. To illustrate these different categories, consider a simple scenario: you and a friend are deciding where to dine.

This decision-making process can be easily translated into programming language. Imagine you’re tasked with adding new features to a project. How straightforward will it be to implement a particular feature? Ultimately, it's akin to the dining decision.

Easy Problems (P)

You and your friend are both hungry. You propose pizza, but your friend is not in the mood. They suggest sushi, yet raw fish doesn't appeal to you. After a series of suggestions, you finally say, "Let’s opt for the closest option." You begin evaluating the top choices based on their proximity to your location.

Mathematically, this situation can be represented as Y(time to reach the restaurant) = 10 X(distance to the restaurant), where 10 denotes the minutes required to walk 1 km. This type of equation is referred to as polynomial. Thus, the term Polynomial-time emerges. Problems classified as P are typically mundane, but they include common scenarios like sorting and searching algorithms.

Hard Problems (EXP)

Now, let’s complicate matters. Imagine that your parents and siblings are joining you for dinner. You can still use the same approach of going to the nearest restaurant, or you can explore more efficient solutions. You might ask everyone what they want to eat and encourage them to agree on a single option.

In the P scenario, each individual picked one place, and the closest was chosen. However, now each person has to make multiple decisions, leading to increased complexity. In mathematical terms, we describe this as Y(time needed to decide) = X², where X is the number of people involved. This represents an exponential (EXP) problem, which generally requires more time to solve than the P approach.

Solvable Problems (R)

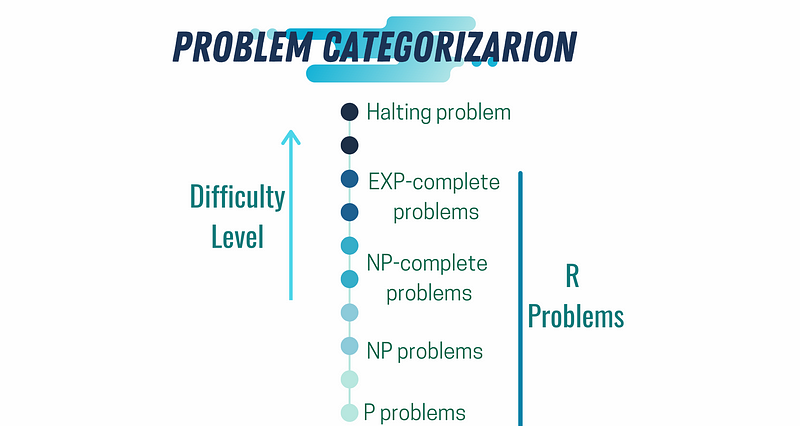
Despite the time it takes to decide on a meal, you ultimately reach a conclusion and eat—this characterizes solvable problems. R problems are those that can be resolved in a finite timeframe. Whether it takes seconds, hours, or days, as long as it’s finite, the problem is solvable.

You might wonder if there's a problem that requires infinite time to solve. Indeed, the halting problem exemplifies this. It questions whether we can design a general algorithm that determines if a specific program will halt given a particular input. The term "general" renders this problem unsolvable, as we cannot predict program halting without execution.

This video titled "The Complexity Class P - Complexity Theory" provides a deeper dive into the nuances of complexity classes and their implications in computer science.

Deterministic vs. Nondeterministic Approaches

When coding to solve a problem, we often follow a deterministic approach—using a series of loops and conditional statements. An alternative is the nondeterministic approach, which involves asking questions or making guesses until reaching a solution.

Returning to the dining dilemma, suppose instead of evaluating options based on distance, you wrote down the choices and allowed your cat to decide. By placing the options in front of the cat and observing its choice, you’ve resolved the issue in a nondeterministic manner. This technique expedites the resolution of P-type problems using a magical, nondeterministic approach, classifying them as NP problems.

Does P Equal NP?

Finding a nondeterministic solution can often hinge on luck. Your cat made the decision easier, but not everyone has such an advantage. In computer science, opinions are divided on whether P equals NP. Some believe it’s just a matter of time before we develop nondeterministic methods for all P problems, while others maintain that certain problems are inherently unsolvable in a nondeterministic fashion. The truth remains uncertain; only time will tell.

Exploring NP Problems

One of the most intriguing categories in computer science is NP problems. In 1970, Richard Karp demonstrated that all SAT (Satisfiability) problems could be reduced to NP and compiled a list of 21 NP-complete problems. If you’ve encountered this list, you might have noted that while these problems are classified as unsolvable, some solutions exist in textbooks. The traveling salesman problem, for instance, is considered NP-hard, yet approximate solutions can address specific scenarios.

NP-hard vs. NP-complete

Any NP problem that can be solved nondeterministically in P time qualifies as an NP-complete problem, provided it’s a decision problem. NP-hard problems are a step further; they can be reduced to NP-complete problems in P time but are not necessarily decision problems, such as the halting problem.

Conclusion

Complexity theory is a vital area within computer science that focuses on categorizing problems based on the time required for their resolution. Importantly, complexity theory prioritizes the nature of the problem itself over the algorithms employed.

We frequently encounter NP-hard and NP-complete problems more often than we realize. Understanding how to categorize and analyze these issues can help us devise more effective solutions or transform them into P-type problems to suit our requirements. A robust grasp of complexity theory and its various classifications will undoubtedly enhance your work and potentially lead to significant breakthroughs.

The video "What is Complexity Theory?" serves as an excellent introduction to the foundational concepts and implications of complexity theory in computer science.