Chapter 1: The Pythagorean Theorem Explained

The Pythagorean theorem establishes a fundamental relationship in right-angled triangles: the sum of the squares of the two shorter sides equals the square of the hypotenuse.

This theorem is foundational across various scientific fields. To illustrate its significance, consider the role of vector notation, which is essential in areas such as classical mechanics, electromagnetism, relativity, and quantum mechanics. Understanding not just how to apply this theorem, but also the reasoning behind its validity, is crucial.

To visualize this, let’s consider a sector that we can split into two segments, designated as a and b, representing the legs of a right triangle.

Now, we introduce the hypotenuse, which requires us to think in two dimensions. We can conceptualize the combined length of sides a and b as the side of a square.

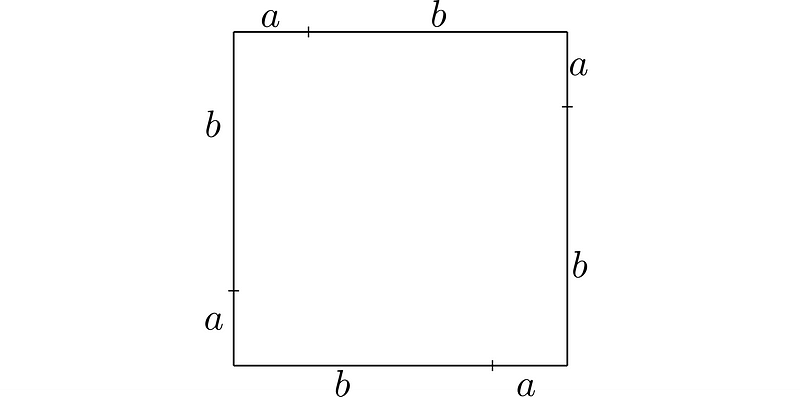
The area of this square is calculated as side times side, leading us to the following:

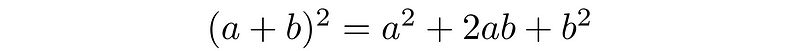
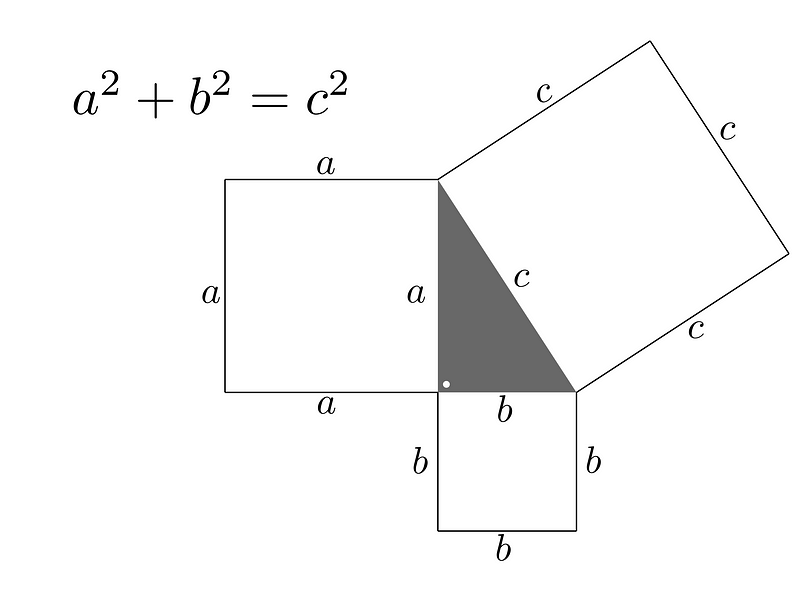
Next, we can create our triangle by partitioning this area into smaller sections:

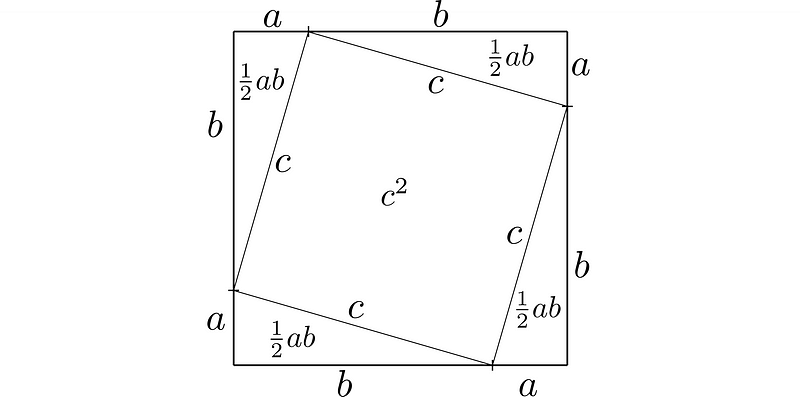
This results in four congruent right triangles with sides a, b, and c, along with a square having side c. The total area of this configuration is represented as:

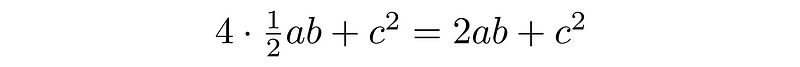
By arranging these triangles and the square, we can confirm that the collective area matches the original square’s area.

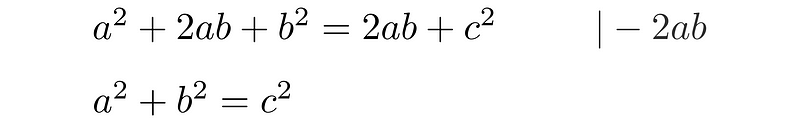
This demonstrates the validity of the Pythagorean theorem. But how does this concept extend into higher dimensions?

To explore how this two-dimensional theorem generalizes, we can consider a three-dimensional scenario. We need a coordinate system and a vector to illustrate this.

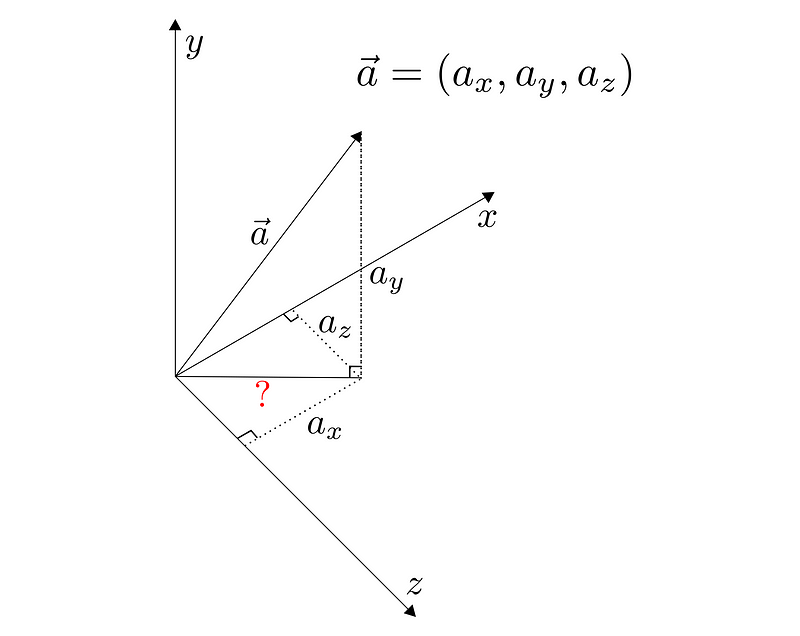
To determine the length of a vector in three-dimensional space, we need to find a right triangle. The projection of any vector component is always perpendicular to the plane it intersects, ensuring that each axis remains orthogonal to the others.

What are the implications of this? The y-component, which extends our 2D space into the third dimension, is perpendicular to the xz-plane. By finding the magnitude of the vector from the origin to the intersection point with this plane, we can form our triangle and utilize the theorem.

The x and z components intersect at right angles, allowing us to visualize them as forming a rectangle. The diagonal of this rectangle corresponds to the vector that shares components along the xz-plane with our a-vector, thus dividing it into two right triangles. We can apply the Pythagorean theorem to ascertain its magnitude:

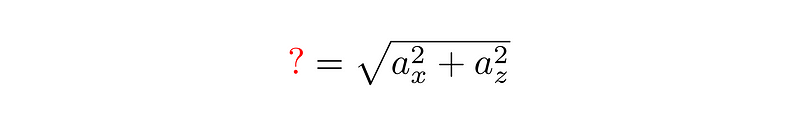
At this point, we have both sides of our right triangle established. The first side is the length we calculated earlier, while the second side is the y-component.

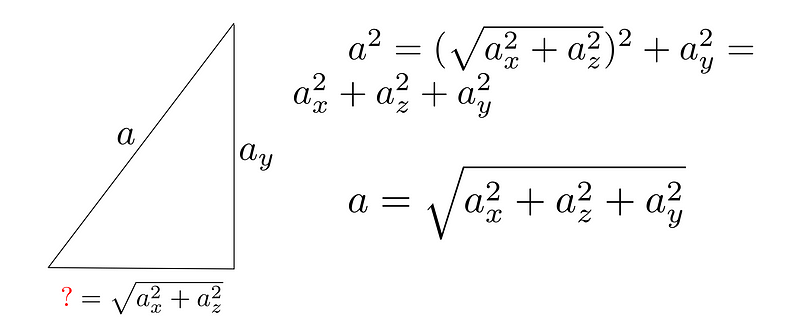
This approach can be extended into even higher dimensions. In an n-dimensional space, when calculating the magnitude of a vector, we can also decompose it into two parts. The first part, consisting of n-1 dimensions, allows for the calculation of the diagonal of a hyperrectangle, which serves as one side of the desired right triangle. The remaining dimension provides the nth dimension, which completes the second side of the right triangle. In essence, regardless of the dimensionality of your coordinate system, the Pythagorean theorem remains applicable.

The formula for higher dimensions can be expressed as follows:

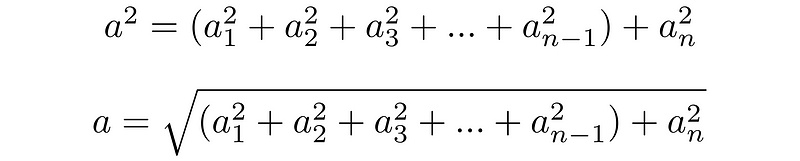
Chapter 2: Proving the Pythagorean Theorem

To further understand the theorem, we can explore some engaging videos that delve into its proof.

The first video, titled "18 Year Old Students Just Discovered a Proof of Pythagoras That Mathematicians Said Was Impossible," showcases young minds tackling complex mathematical challenges.

The second video, "Proving the Pythagorean Theorem," offers a detailed examination of the theorem's proof and applications.