Unlocking the Secrets of Square Roots: Hero of Alexandria's Legacy
Written on
Introduction to Hero of Alexandria
Throughout history, certain individuals have made contributions that resonate beyond their era, shaping future generations. One such figure is Hero of Alexandria, a prominent mathematician and engineer of the 1st century AD. His innovative designs and mathematical insights have created a lasting influence that continues to motivate and challenge thinkers and engineers today.
Hero’s Engineering Innovations
Steam Engine:
Among Hero’s notable inventions is the aeolipile, regarded as a precursor to the contemporary steam engine. This device functioned on the principles of jet propulsion, where steam was expelled through nozzles to produce motion. While it wasn’t utilized in his time, it laid essential groundwork for future steam-powered technologies.
Automatic Doors:
Hero’s creativity also extended to more mundane aspects of life with his creation of automatic doors. By employing a mechanism of weights, ropes, and pulleys, these doors opened in response to an individual’s approach, foreshadowing modern sensor-based systems.
Heron’s Fountain:
Known as the Fountain of Alexandria, Hero’s Heron’s fountain demonstrated his profound understanding of fluid dynamics. It utilized siphon principles, showcasing his ability to manipulate water pressure for a continuous flow.
Hero's Contributions to Mathematics
Geometry:
Hero made substantial advancements in geometry, especially in determining areas and volumes. He developed techniques for calculating the areas of various shapes, including triangles, circles, and even complex irregular polygons.
Heron’s Formula:
One of Hero's most significant contributions is Heron’s formula, which allows for the calculation of a triangle's area when the lengths of its sides are known. This formula remains a staple in geometry education today, reflecting Hero’s deep understanding of mathematical concepts.
Square Roots:
Hero's method for estimating square roots stands as a remarkable achievement of ancient mathematics. This technique facilitates the approximation of square roots without a calculator, demonstrating his mathematical expertise.
Calculating √2 Without a Calculator
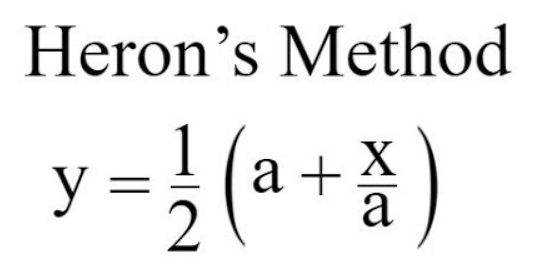
Step 1: Make an Initial Guess
Begin by selecting an initial estimate for the square root. This can be any positive number, ideally one that is close to the true square root. This initial guess will represent the value of ( a ).
Step 2: Apply the Iterative Formula
Utilize Heron’s formula to enhance your approximation:

Substitute your initial guess as ( x_0 ) or ( a ). Calculate ( x_{n+1} ) using the formula.
Example Calculation:
Let’s determine the square root of 2 using Heron’s method:
- Initial guess: ( x_0 = 1 ) (a sensible starting point).
- Apply the formula:

Step 3: Iterate the Process
Repeat the calculation:

Continue this step using 1.41667 as your new value for ( x ) in the formula. The approximation will become increasingly accurate with each iteration. However, be mindful of computational limits and the precision required for your needs.
This method remains highly effective and is frequently employed in computer algorithms and numerical analyses. Even today, institutions like MIT and Caltech teach this approach to illustrate how focused thought can lead to meaningful problem-solving.
Thank you for reading!
Description: This video demonstrates how to calculate square roots mentally, showcasing techniques that reflect Hero of Alexandria's historical contributions.
Description: This video provides a step-by-step guide on finding square roots by hand without a calculator, emphasizing traditional mathematical methods.