The Fascinating Link Between Roots and Logarithms Explained
Written on
Chapter 1: Introduction to Roots and Logarithms
Have you ever wondered why the natural exponential function exhibits periodic behavior with an imaginary period of 2πi? Or why there exists an infinite number of (complex) logarithms for a single number? While it may sound odd, the answer lies in an infinite geometric representation involving circles.
In this article, I will present a geometric and intuitive interpretation of these concepts, followed by a more rigorous examination through limits. What unfolds is a captivating geometric relationship between roots and logarithms that clarifies the periodicity of the exponential function—without relying on Euler’s formula.
Section 1.1: Understanding nth Roots
When we refer to the square root of a positive real number r, we typically mean the positive solution √r that satisfies the equation x² = r. However, this equation actually has two solutions: √r and -√r. Therefore, a positive real number has two real square roots.
In contrast, the case of cube roots is slightly different; there is precisely one real cube root for any real number. Yet, it's misleading to think there is only one cube root—its true nature reveals itself in the complex plane.
Complex numbers can be represented as points within a two-dimensional plane, where the real axis acts as a one-dimensional subset. For example, the point (r, 0) corresponds to the real number r, while the point (a, b) represents the complex number a + bi, with i being the imaginary unit (where i² = -1).
Each point in the complex plane has a modulus (distance from the origin) and an argument (angle in radians) measured from the real axis. For instance, the point representing i is (0, 1), where its modulus is 1 and its argument is π/2 + 2kπ for any integer k.
This multivalued characteristic is crucial because it can lead to significantly different results depending on the values involved.
For example, when we consider the natural logarithm, denoted as ln, asking for the logarithm of a positive real number a typically refers to the unique real number b such that e^b = a. However, similar to roots, there are indeed countless numbers that satisfy this condition, many of which exist beyond the real number line and reside in the realm of complex numbers.
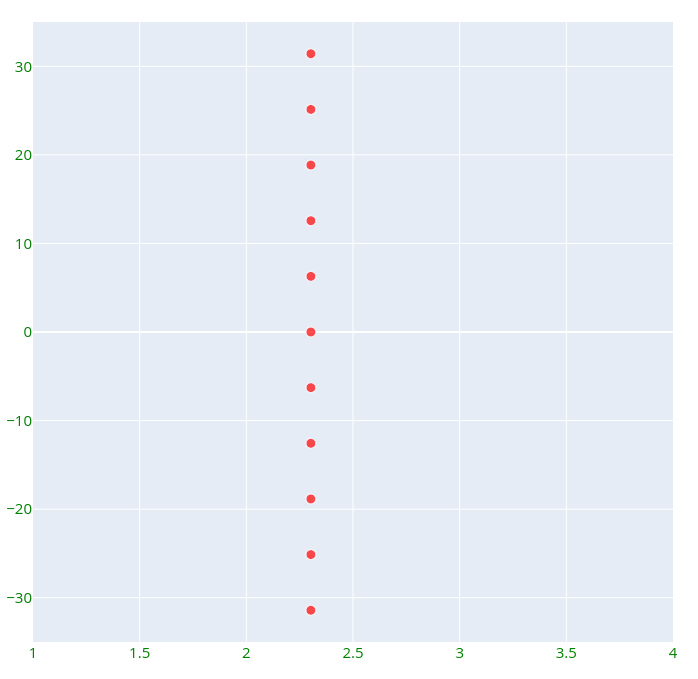
Infinitely many complex numbers satisfy this equation, including ln(a), which can be expressed as ln(a) + 2πik for each integer k. Thus, if we take ln(10) as an example, it appears as follows in the complex plane:
Section 1.2: Visualizing Cube Roots
Similar to logarithms, roots also exhibit multivalued properties. Specifically, any non-zero complex number z has exactly three cube roots. For clarity, we will focus on the roots and logarithms of positive real numbers, though the same principles apply to all complex numbers.
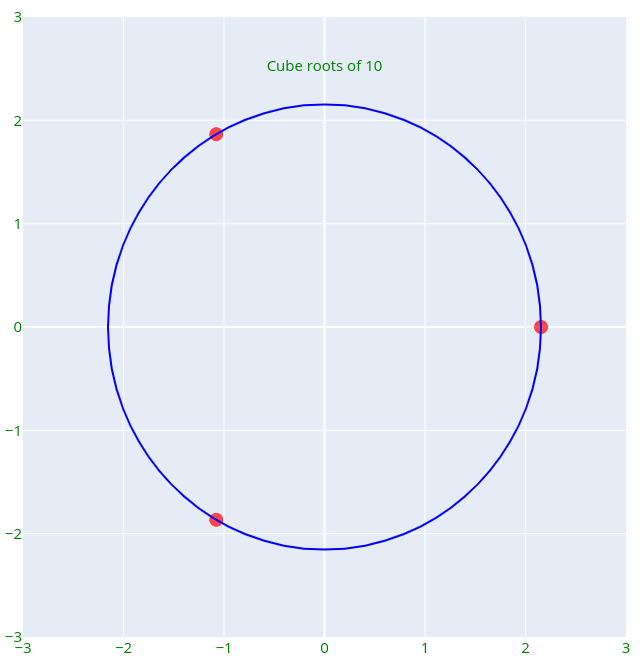
The cube roots of a real number r > 0 correspond to three points in the complex plane that form the vertices of an equilateral triangle inscribed within a circle centered at the origin, with a radius equal to the real cube root of r. For instance, the cube roots of 10 can be depicted as follows:
More generally, the nth roots of a positive real number r create a regular n-gon with vertices evenly distributed along a circle centered at the origin, with a radius equal to the real nth root of r. For instance, the twelve roots of 72 can be represented as:
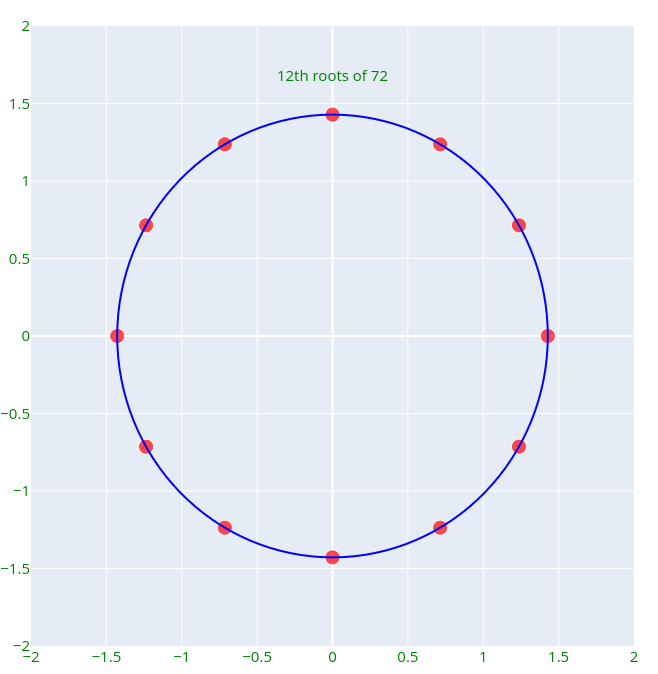
Interestingly, raising any of these complex numbers to the power of 12 yields 72. This distribution explains why we have two real square roots in the forms -√r and √r; they must be evenly placed on a circle of radius √r, necessitating the presence of both solutions.
Chapter 2: The Relationship Between Exponentials and Logarithms
You might wonder how all this relates to logarithms. The purpose of this article is to elucidate the multivalued nature of logarithms, which in turn helps us understand the periodicity of the exponential function. To achieve this, we'll define an intriguing sequence of functions.
For any natural number n, we can define the function:
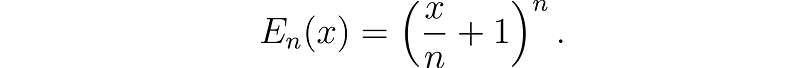
We will also need to find its inverse, which can be expressed as:
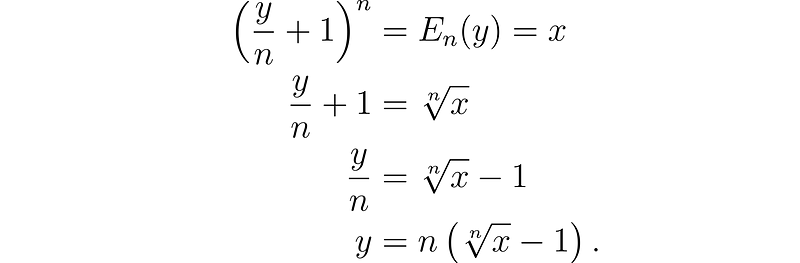
Consequently, we establish another sequence of functions represented as follows:
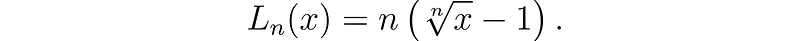
Through these definitions, we can articulate what we mean by the natural exponential function and its inverse—the natural logarithm.

We could also define e^x using a Taylor series, demonstrating that it aligns with the previous definitions. This approach simply depends on personal preference.
Note that we haven't explicitly defined what we mean by the nth root in the L_n definition; it's evident that any of the n roots will establish an inverse function to E_n.
To grasp the broader context, we will consider all of them! For any given value of x, E_n(x) will approximate e^x as n increases. However, what happens to the nth roots within the L_n(x) expression?
Assuming x > 0, at least one of the roots will converge toward the real number ln(x). Let's visualize this for x = 10 while varying n.
Examining L_n(x) after expanding the expressions illustrates that n values of this function will still form a circle. The following plot depicts the values of L_12(10) as a multivalued function:

Increasing n to 30 results in the following visualization. Note how the circle expands in size:
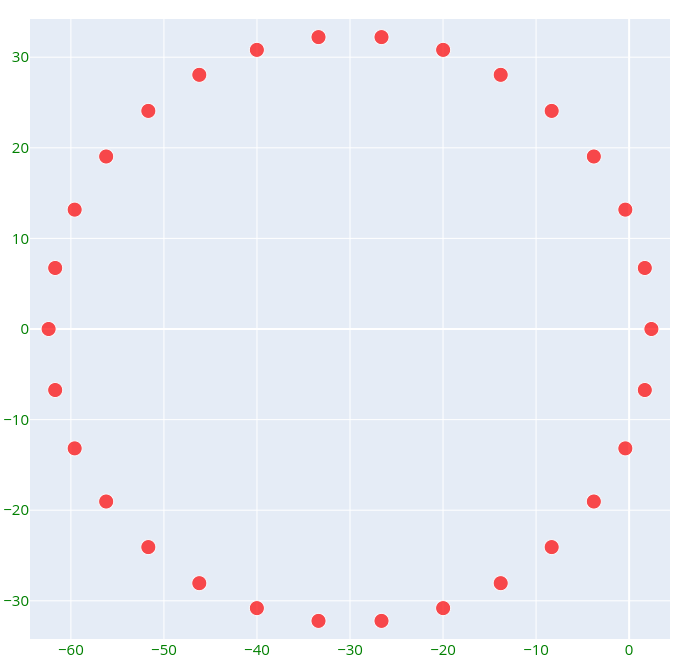
When we let n approach 1000 and zoom in on the right arc, we observe:
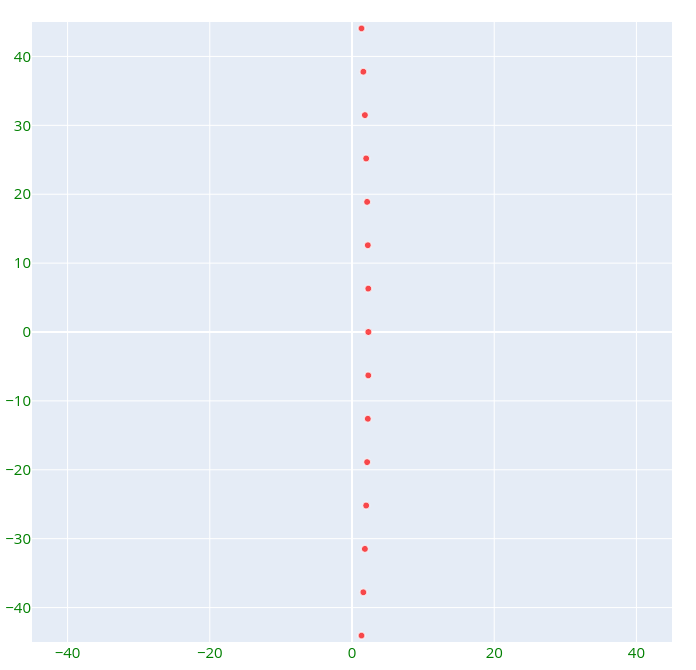
The points nearly align on a vertical line, remaining equally distributed. As n increases, the distance between them appears to approach 2π. Ultimately, as n approaches infinity, the only points that remain finite are those aligned along this vertical line in the limit.
This illustrates why the logarithm of a number x possesses infinitely many equivalent values z_m (in the sense that they all satisfy e^(z_m) = x) and maintain equal spacing from their neighbors. They are distributed evenly on an infinitely large circle within the complex plane!
This, in turn, elucidates why the exponential function possesses a purely imaginary period.
Section 2.1: The Form of Logarithmic Values
Let’s establish that all equivalent logarithmic values of x can be represented as ln(x) + 2kπi through a geometrically motivated approach.
The initial step involves expressing all n points as defined by the function L_n(x). These points are represented by complex numbers as follows:
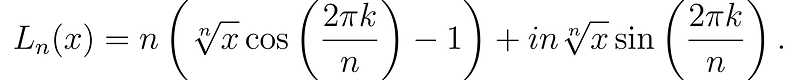
As n approaches infinity, cos(2πk/n) approaches 1, leading the real part of this expression to converge on ln(x). The next step is to compute the limit of the imaginary part as n approaches infinity.
Using L'Hôpital's rule, we arrive at the following calculation:
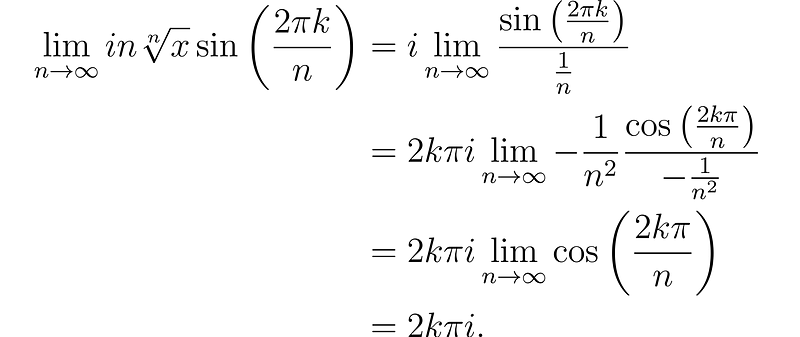
As the real nth root of x approaches 1 as n approaches infinity, we can exclude it from consideration. This clearly demonstrates the origin of the exponential function's periodic nature—it results from the limit of a dilation and translation of roots around a circle, which ultimately transforms into a line in the complex plane.
Final Thoughts
The standard methodology for tackling multivalued functions often involves the application of branch cuts and principal values, or even Riemann surfaces. However, I find the multivalued nature intriguing because it enables us to address all scenarios collectively.
We must exercise caution, though. Just as we need a clear understanding of what we mean by √r and ln(a) as symbols, we must also clarify our intentions.
For example, if your problem is strictly real, then ln(a) is likely meant to be real. However, if you're dealing with complex numbers, especially when solving equations involving the complex exponential function, things become less straightforward.
Consider the well-known equation e^(iπ) = -1. Does this imply that ln(-1) = iπ? It depends on how we define the logarithm. We can establish infinitely many logarithms. The principal logarithm, for example, confines its imaginary part within the interval (-π, π], yielding Log(-1) = iπ. Alternatively, we could define a different logarithm that results in log(-1) = -iπ. In either scenario, we would still have e^Log(-1) = e^log(-1) = -1, which is consistent.
Any logarithm should possess the value log(-1) = (π + 2kπ)i for some integer k, and the multivalued definition encompasses all such values. The challenge lies in converting this into a continuous function, but we’ll leave it here for your contemplation.
This inversion problem is also present in many other renowned functions, including the "inverse" trigonometric functions, for instance.
If you enjoy articles like this, consider subscribing to gain full access to similar content on Medium. Thank you for reading!
Chapter 3: Video Resources
To further understand the concepts discussed, check out the following videos:
This video titled "How To Evaluate a Logarithm To a Square Root of a Number Without a Calculator" provides insights into evaluating logarithms in a straightforward manner.
In this video titled "LOGARITHMS | Where They Come From & Why We Use Them," you'll discover the origins and applications of logarithms, deepening your comprehension of the material covered.