Chapter 1 Understanding Square Roots

The concept of a square root involves identifying a number that, when multiplied by itself, yields the original number. Squaring that square root will bring us back to the initial value. This principle serves as the key to solving today’s intriguing problem.

Before diving in, I suggest pausing here to grab a pen and paper. Once you're prepared, let’s continue to explore the solution!

Solution Strategy

Our approach will be to square the expression before extracting the square root.

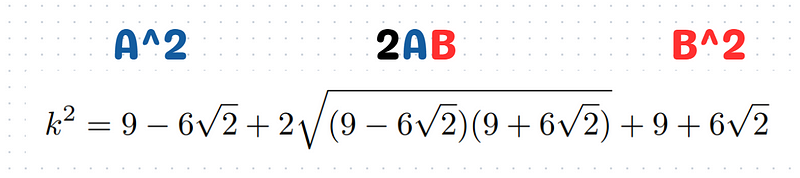
In this scenario, we have ( k² = (A + B)² ), where ( A = sqrt{9 - 6sqrt{2}} ) and ( B = sqrt{9 + 6sqrt{2}} ). The perfect square formula is what we've utilized here. Now, let’s simplify our algebraic expressions.

The result of ( A² - B² ) yields 18, while the number 9 derived from expanding the brackets. Ultimately, since the square root of 9 is 3, we calculate ( 18 + 2(3) = 24 ).

At this stage, our task is to find the square root.

We recognize that ( 24 = 2² times 6 ), leading us to our final answer.

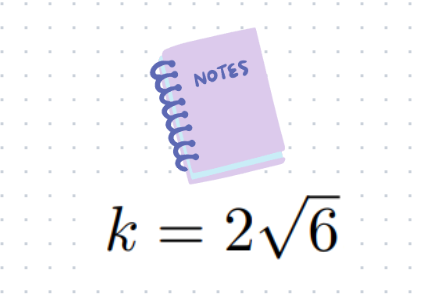
Isn't that fascinating? What was your thought process during this challenge? Feel free to share your insights in the comments below—I’d love to hear from you!

Math Puzzles to Explore

If you enjoyed this puzzle, consider checking out the following collection of math challenges available on Medium.

Can you solve the never-ending square root? - This video invites you to engage with a captivating square root problem.

Are you smart enough to crack this? - A fun challenge featuring various math concepts that are sure to test your skills!

Thank you for taking the time to read this article. If you found it helpful, please give it a clap!

If you appreciate the effort put into creating this content, consider buying me a coffee! Your support means a lot to my writing journey.

With gratitude, Bella