The Significance of Harmonic Numbers and Their Approximations
Written on
Understanding Harmonic Numbers
If you frequently engage with literature in Mathematics, Computer Science, or related disciplines, you may have encountered the concept of the harmonic sum, defined as follows:
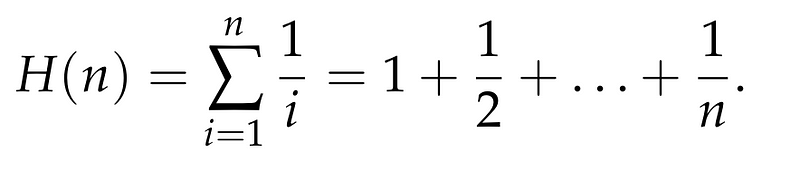
The notation H(n) represents the n-th Harmonic Number. These numbers not only find applications in various fields (as illustrated in a previous discussion on the Coupon Collector problem, where an expected value involves a harmonic sum), but they also pique the interest of mathematicians due to their inherent properties. This article aims to provide a reliable estimate for H(n).
Computational Insights
We begin with a straightforward observation: each term in the harmonic sum can be visualized as a rectangle with a width of 1 and a height of 1/i. Hence, H(n) can be interpreted as the cumulative area of specific rectangles, represented by the yellow area in the following illustration.
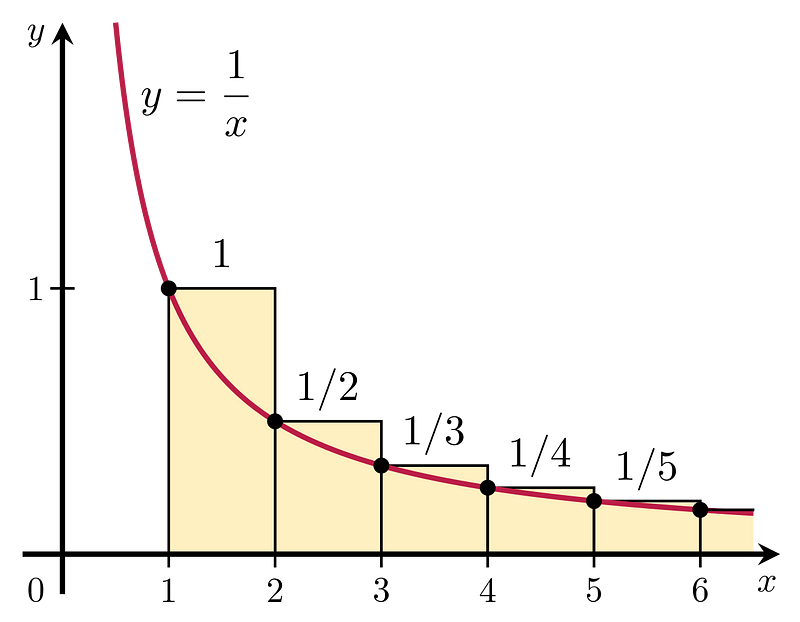
Notice how the rectangles are arranged so that the graph of the function f(x) = 1/x for x ≥ 1 intersects the top left corner of each rectangle, remaining within the yellow area. This indicates that H(n) equals the total area of the first n rectangles shown. From this, we can deduce that the yellow area is at least as expansive as the area under the red line, meaning it is also greater than the area between the graph of f(x) = 1/x and the x-axis:
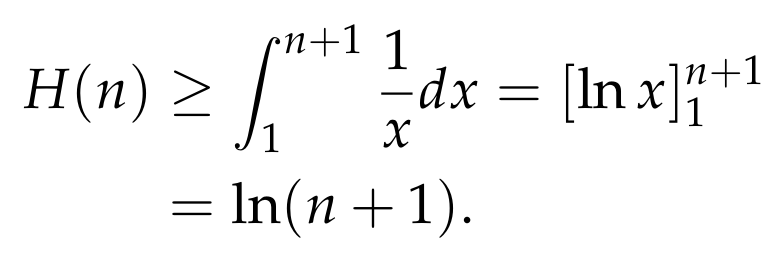
This already provides a good lower estimate, particularly indicating that as n increases, H(n) becomes unbounded, confirming that the harmonic series diverges:

However, we seek a more precise approximation. By adjusting the rectangles to ignore the first term and shifting them one unit left, we can observe that the function f(x) = 1/x encompasses at least as much area as the remaining rectangles. This is visually represented below.
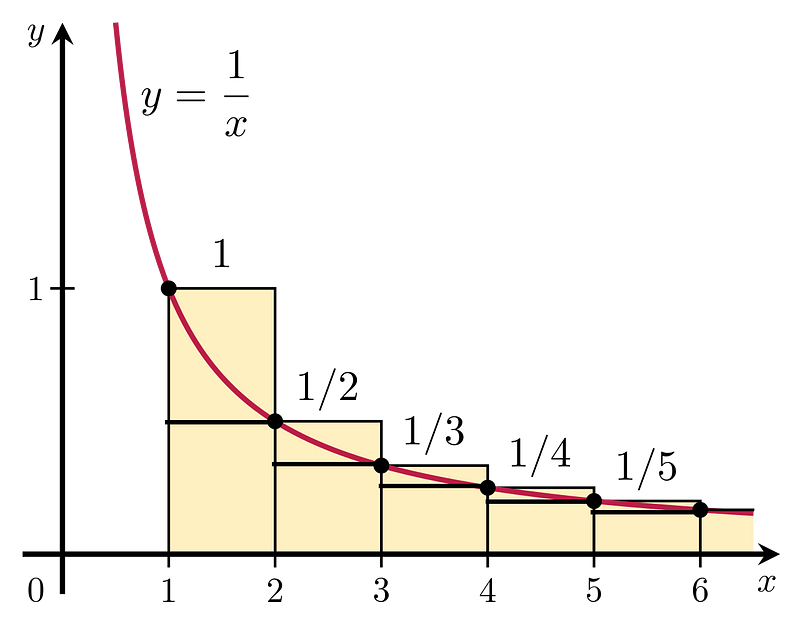
From the above figure, we conclude:

This leads us to establish that

Specifically, we find that
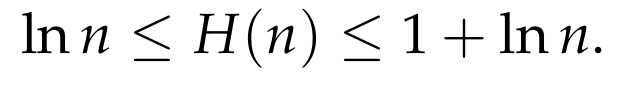
These bounds indicate that for any n, if we compute ln(n) instead of H(n), our error will be no greater than 1.
Refining the Approximation
With much more extensive analysis (beyond the scope of this article), it can be shown that the error term in the approximation converges to a constant that is actually smaller than 1. This constant is known as the Euler-Mascheroni constant, formally defined as:
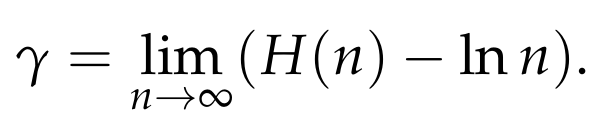
The first 50 digits of this constant are:
γ = 0.57721566490153286060651209008240243104215933593992.
Using this constant, it can be demonstrated that the n-th Harmonic Number is effectively represented as:
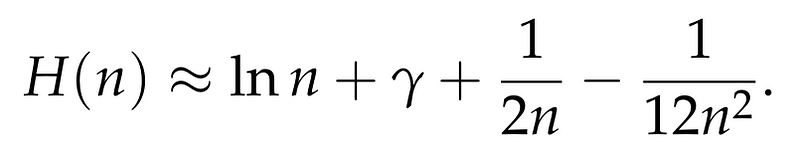
Conclusion
In this discussion, we explored the well-known harmonic sum and the corresponding sequence H(n). We illustrated how these numbers behave similarly to the sequence {ln n} for n = 1, ….
Numerous resources online elaborate on the approximation of the harmonic sum, and readers are encouraged to delve deeper into the Euler-Mascheroni constant, whose algebraic or transcendental nature remains an open question, and even its irrationality is still uncertain.
References
This video titled "Extending the Harmonic Numbers to the Reals" provides a deeper understanding of harmonic numbers and their extensions.
The video "Harmonic Series - Part 4 - Approximation" further explores the methods of approximating the harmonic series.