Chapter 1: Introduction to Integral Equations

In a 2011 study by Waldemar Klobus titled "Motion on a Vertical Loop with Friction," an intriguing integral equation, specifically a Volterra integral equation of the second kind, is introduced. This equation describes the dynamics of an object traversing a circular loop, as depicted in the figures below:

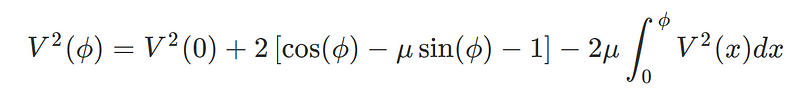
The equation illustrates how the coefficient of friction affects the tangential frictional force experienced by the object. Here, V represents the normalized speed of the object, defined by the square root of ( gR ), where ( g ) signifies gravitational acceleration and ( R ) is the loop's radius. Although the paper provides a solution to the equation, it does not elaborate on the resolution process. This article will detail a step-by-step derivation of the solution. It's worth noting that ( V(0) ) is a constant defined in the original paper based on certain critical conditions; however, my focus will primarily be on the general solution for the equation.

This integral equation can be approached through a straightforward technique involving differentiation. For instance, differentiating the first equation yields:

This result can be succinctly expressed as:

Now, this reformulated equation becomes a first-order differential equation for ( V^2 ) with linear properties and constant coefficients, allowing for a precise closed-form solution. By applying the integrating factor method, we integrate the function adjacent to the ( V^2 ) term on the left-hand side (LHS) and express it in an exponential format:

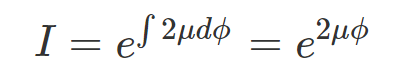
Next, we multiply both sides of the equation by this integrating factor:

Utilizing the chain rule of differentiation allows us to rewrite the LHS in the following manner:

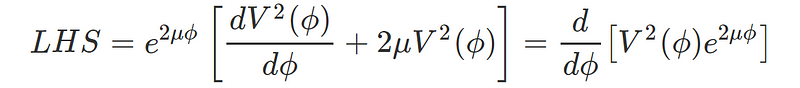
Thus, our equation transforms into:

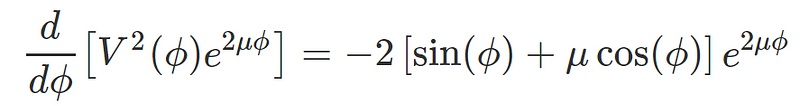
Next, we integrate the equation concerning ( phi ), selecting a "dummy integration variable" ( t ) and performing the integration from 0 to ( phi ):

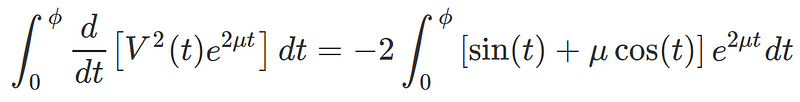
The LHS of this equation integrates readily to yield:

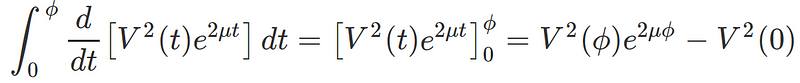
The right-hand side (RHS) can be evaluated using conventional integration techniques, such as integration by parts:

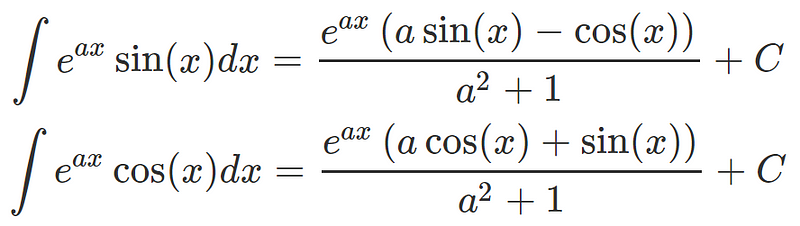
Consequently, we derive the RHS as follows:

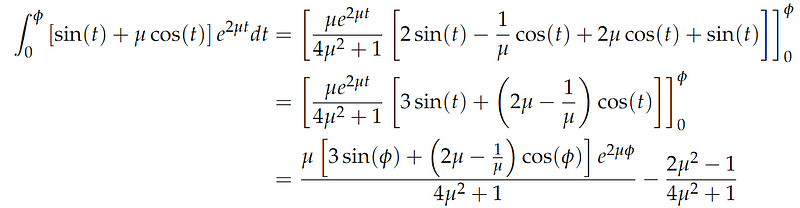
By combining the results from both sides, we can summarize the findings as:

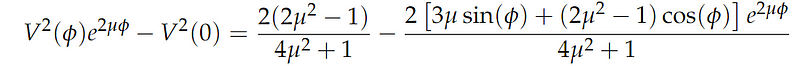
Rearranging the equation yields:

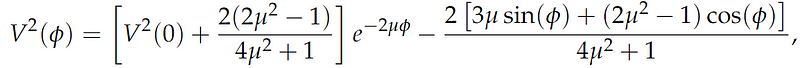
Finally, by substituting the necessary variables, we arrive at the solution format presented in the original paper:

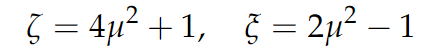
Chapter 2: The Power of Differentiation

The fascinating aspect of this problem is that we achieved a relatively simple yet precise solution to the integral equation by initially applying differentiation. Often, straightforward steps like these can significantly ease the process of solving complex mathematical challenges.

A comprehensive guide to solving integral equations using differentiation.

Discover integration tricks that can simplify your calculus problems.